甲和乙各有9粒彈珠和3個相同的箱子，他們須把自己的9粒彈珠分配到自己的3個箱子，每個箱子至少要放有1粒彈珠。然後每人各自隨機抽出一個箱子，誰箱子裏的彈珠較多便勝出。若雙方的彈珠數量相同，每人則再次各自隨機抽出一個箱子，直至有一人勝出為止。若甲在選擇前已知道乙的選擇策略，求乙的最佳策略。

解：

設(a,b,c)為第一個箱子放a粒彈珠、第二個箱子放b粒彈珠、第三個箱子放c粒彈珠。

分配的所有可能性為：(1,1,7), (1,2,6), (1,3,5), (1,4,4), (2,2,5), (2,3,4), (3,3,3)

下表列出不同情況下乙勝出（左）和敗局（右）的可能數量（和局會重來，其數值並不重要）：

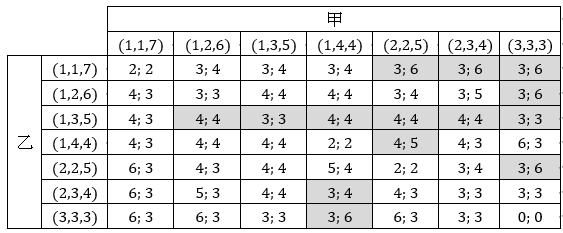
有底色為對甲根據乙的選擇時最有利的選項。

乙的最佳策略為必選(1,3,5)，即三個箱子分別放1粒、3粒和5粒彈珠，可使甲無論作任何選擇，其勝率均不超過一半。

以上情境可用小學奧數的技巧，避免複雜的概率和期望值運算。至於若把9粒彈珠改為10粒彈珠，則需要用到更高級的數學知識，可於谷歌圖書搜尋「分配博奕中劣勢方的最佳策略情境範例」。